Dopełnienie zbioru przykłady – kluczowe koncepcje w teorii zbiorów

Co to jest dopełnienie zbioru?

Dopełnienie zbioru A, oznaczane jako A’ lub Aᶜ, odnosi się do wszystkich elementów, które znajdują się w uniwersum, ale nie są uwzględnione w zbiorze A. Uniwersum stanowi kontekst, w którym pracujemy, a konkretna definicja dopełnienia zależy od tego, co rozumiemy przez to uniwersum.

Weźmy za przykład sytuację, gdy uniwersum obejmuje liczby całkowite, a zbiór A zawiera liczby parzyste; w takim przypadku dopełnienie A to liczby nieparzyste. Użycie symboli A’ i Aᶜ w matematyce pomaga w łatwym zaznaczeniu elementów, które są wykluczone z danego zbioru.

Zrozumienie dopełnienia jest niezwykle ważne dla analizowania relacji pomiędzy różnymi podzbiorami. Możemy je obliczyć, identyfikując te wszystkie elementy, które nie są częścią zbioru A w ramach ustalonego uniwersum. Dla przykładu, w kontekście liczb naturalnych, jeżeli zbiór A jest równy {1, 2, 3}, to dopełnienie A składa się z pozostałych liczb naturalnych, jak np. {4, 5, 6,…}.

Narzędzie to ma ogromne znaczenie w teorii zbiorów oraz w różnych innych obszarach matematyki. Zrozumienie, w jaki sposób zbiory oddziałują ze sobą, jest kluczowe dla bardziej zaawansowanej analizy.

Jakie są definicje dopełnienia zbioru?

Dopełnienie zbioru to istotny koncept, który odnosi się do związku między danym zbiorem a jego uniwersum. Wskazuje ono na wszystkie elementy, które należą do uniwersum U (lub Ω), ale nie znajdują się w zbiorze A. Formalnie dopełnienie A symbolizujemy jako A’ = U \ A lub A’ = Ω \ A. W praktyce dopełnienie obejmuje te elementy, które są poza zbiorem A, ale wciąż znajdują się w określonej przestrzeni.

Na przykład, kiedy uniwersum stanowią liczby całkowite, a zbiór A to liczby parzyste, wówczas dopełnieniem A będą liczby nieparzyste. Zrozumienie tego pojęcia jest kluczowe nie tylko w teorii zbiorów, ale także w analizie struktur matematycznych.

Użycie notacji A’ i Aᶜ w obliczeniach zbiorowych umożliwia dokładne wskazanie elementów wykluczonych z danego zbioru. Dla przykładu, przyjmując A = {1, 2, 3}, dopełnienie względem zbioru liczb naturalnych obejmuje elementy takie jak {4, 5, 6,…}. Tego typu analiza prowadzi do głębszego wnikania w relacje oraz interakcje między różnymi zbiorami, co stwarza warunki do zaawansowanej analizy w różnych obszarach matematyki.

Jakie symbole oznaczają dopełnienie zbioru?

Dopełnienie zbioru najczęściej przedstawiane jest jako A’ (czytane jako 'A prim’) lub Aᶜ (wymowa: 'A dopełnienie’). Oba te symbole znajdują uznanie w literaturze matematycznej, choć różnią się zastosowaniem. Zapis A’ jest powszechnie stosowany w teorii mnogości oraz analizie matematycznej, natomiast Aᶜ dominuje w algebrze zbiorów i prawdopodobieństwie.

Można również spotkać oznaczenie −A, które jednak występuje rzadziej i może wprowadzać pewne zamieszanie. Z tej przyczyny kluczowe jest, aby znajomość odpowiednich symboli pozwalała na precyzyjne określenie elementów, które nie należą do danego zbioru.

Rozpoznanie różnic między A’ a Aᶜ ułatwia ich praktyczne zastosowanie, na przykład w kontekście zadań dotyczących prawdopodobieństwa czy w analizach logicznych związanych ze zbiorami. Odpowiednie zdefiniowanie symboli jest fundamentem dalszych działań w matematyce.

Jakie są własności dopełnienia zbioru?

Właściwości dopełnienia zbioru stanowią kluczowy aspekt teorii zbiorów. Na początek warto zauważyć, że suma zbioru A oraz jego dopełnienia A’ zawsze prowadzi do stworzenia zbioru uniwersalnego, co wyrażamy jako A ∪ A’ = U (bądź Ω). Dodatkowo, przecięcie zbioru A z jego dopełnieniem A’ daje nam zbiór pusty, czyli A ∩ A’ = ∅. Kolejną istotną cechą jest fakt, iż dopełnienie zbioru uniwersalnego wynosi zbiór pusty: U’ = ∅, natomiast dopełnienie zbioru, który nie zawiera żadnych elementów, prowadzi nas z powrotem do zbioru uniwersalnego: ∅’ = U. Również warto zwrócić uwagę na zasadę inwolucji: dopełnienie dopełnienia zbioru A zawsze równa się z powrotem zbiorowi A, co możemy zapisać jako (A’)’ = A.

Oprócz tego, prawa de Morgana ukazują interesujące związki między dopełnieniami sum oraz przecięć zbiorów. Przykładowo, dopełnienie sumy zbiorów A i B odpowiada przecięciu ich dopełnień, co matematycznie zapisuje się jako (A ∪ B)’ = A’ ∩ B’. Te fundamentalne własności stanowią podstawę algebry zbiorów, umożliwiając realizację bardziej złożonych operacji oraz wspierając analizy, które prowadzą do głębszych odkryć w dziedzinie matematyki.

Od czego zależy dopełnienie zbioru?

Dopełnienie zbioru w dużej mierze zależy od wyboru przestrzeni, którą nazywamy uniwersum, oznaczanym jako U lub Ω. Uniwersum stanowi zbiór, w obrębie którego analizujemy inne kolekcje. Zmiana uniwersum prowadzi do modyfikacji charakterystyki dopełnienia danego zbioru.

Przykładowo, kiedy uniwersum ogranicza się do liczb naturalnych, dopełnienie zbioru liczb parzystych obejmuje liczby nieparzyste. W kontekście liczb rzeczywistych zaś, dopełnienie będzie zawierać zarówno liczby nieparzyste, jak i niewymierne.

Te ilustracje podkreślają, jak kluczowy jest wybór przestrzeni dla prawidłowej analizy zbiorów. Jeśli ograniczymy uniwersum do zbioru {1, 2, 3, 4, 5}, a zbiór A wynosi {2, 4}, to w takim przypadku dopełnienie A w tym uniwersum stanie się {1, 3, 5}.

To, jak zmienimy uniwersum, znacząco wpływa na zbiór dopełniający, co wskazuje na konieczność zrozumienia, w jakich granicach operujemy. Z taką wiedzą będziemy w stanie poprawnie zidentyfikować, które elementy nie są częścią zbioru A.

Można zatem stwierdzić, że rodzaj uniwersum oraz definicje zbiorów mają bezpośredni wpływ na ich cechy dopełnień.

Jakie są elementy dopełnienia zbioru A względem X?

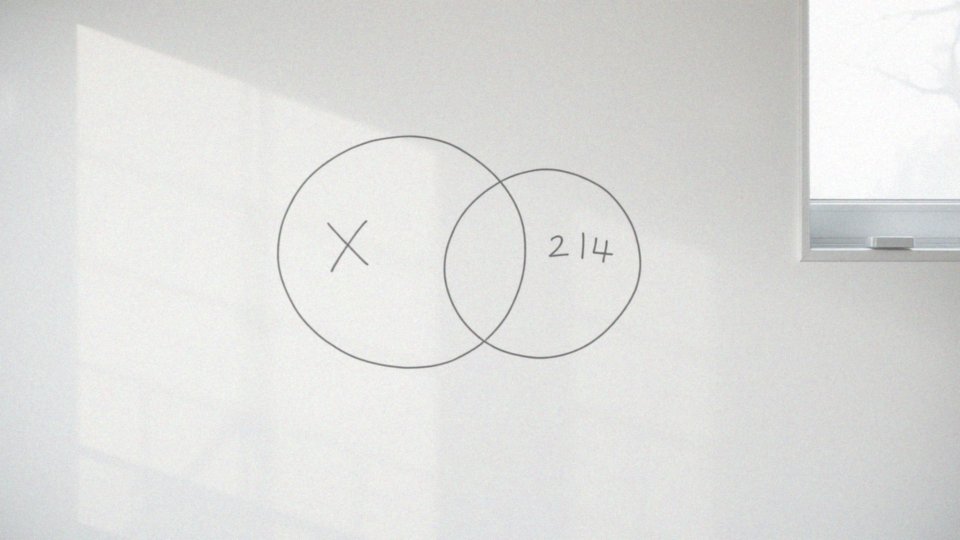
Elementy, które tworzą dopełnienie zbioru A względem zbioru X, to te, które są obecne w zbiorze X, ale nie w zbiorze A. Można to zapisać jako A’ = X \ A, gdzie A’ oznacza dopełnienie zbioru A.

Na przykład, gdy mamy zbiór X składający się z:

• {1, 2, 3, 4, 5},
• oraz zbiór A zawierający {1, 3, 5},

to dopełnienie A w kontekście zbioru X będzie wyglądać następująco: {2, 4}. W widoczny sposób, elementy 2 i 4 są zawarte w zbiorze X, lecz nie występują w zbiorze A.

Zrozumienie tej koncepcji ma kluczowe znaczenie dla analizy relacji między różnymi podzbiorami. Dodatkowo, warto zauważyć, że dopełnienie zbioru A zmienia się w zależności od przyjętego uniwersum. Na przykład, gdy uniwersum prezentuje się jako {1, 2, 3, 4, 5, 6}, dopełnienie zbioru A będzie miało inną postać. Takie zjawisko podkreśla, jak istotny jest kontekst, w którym działamy, dla prawidłowego określenia elementów dopełnienia.

Jak obliczyć dopełnienie zbioru A względem zbioru X?

Aby obliczyć dopełnienie zbioru A względem zbioru X, należy zidentyfikować te elementy, które są obecne w zbiorze X, ale nie występują w zbiorze A. Tę operację można zapisać jako A’ = X \ A, co odnosi się do różnicy pomiędzy nimi.

Na przykład, jeżeli zbiór X zawiera liczby:

• 1,
• 2,
• 3,
• 4,
• 5.

a zbiór A składa się z:

• 1,
• 3,
• 5.

To dopełnienie A w tym przypadku to A’ = {2, 4}. Wynika to z tego, że jedynie te elementy z X nie znajdują się w A. Aby obliczyć dopełnienie, wystarczy odjąć elementy zbioru A od zbioru X. Reszta tworzy zatem zbiór dopełniający.

Taka metoda jest bardzo efektywna; można po prostu spisać wszystkie elementy zbioru X, a następnie wyeliminować te, które są częścią zbioru A. Warto zwrócić uwagę, że obliczanie dopełnienia ma kluczowe znaczenie w analizach statystycznych oraz w rozważaniach logicznych. Zmiana uniwersum ma wpływ na końcowy rezultat, co jeszcze bardziej podkreśla istotę rozumienia kontekstu, w którym działamy.

Jakie działania jednoargumentowe ilustrują definicję dopełnienia?

Działania jednoargumentowe, takie jak dopełnienie zbioru, odgrywają kluczową rolę w matematyce, zwłaszcza w teorii zbiorów. Czym tak naprawdę jest dopełnienie? To zbiór wszystkich elementów znajdujących się w przestrzeni uniwersalnej, które nie są częścią konkretnego zbioru. Wśród innych tego typu operacji można wymienić:

• negację logiczną,
• obliczenia związane z funkcjami trygonometrycznymi.

Wszystkie te operacje wykorzystują tylko jeden argument, co czyni je niezwykle efektywnymi narzędziami do analizy w matematyce. Istotne jest, aby zrozumieć, jak kontekst uniwersum wpływa na wyniki tych działań. Na przykład, jeżeli rozważamy zbiór liczb całkowitych, dopełnienie zbioru liczb parzystych składa się z liczb nieparzystych. W podobny sposób, aby obliczyć sinus lub cosinus, wystarczy tylko wartość kąta. Te przykłady podkreślają znaczenie dopełnienia w różnych branżach matematyki wyższej, gdzie zbiory stają się coraz bardziej złożone i wymagające.

Jakie są różnice między dopełnieniem a innymi operacjami na zbiorach?

Dopełnienie zbioru wyróżnia się spośród innych operacji, takich jak suma, różnica czy przecięcie. Jego odmienność polega na specyficznej funkcji, jaką pełni w teorii zbiorów. Operacja ta jest jednoargumentowa, co oznacza, że dotyczy tylko jednego zestawu i jego uniwersum. Dla porównania, operacje takie jak:

• suma (A ∪ B),
• różnica (A \ B),
• przecięcie (A ∩ B)

wymagają dwóch zbiorów, by móc przeprowadzić obliczenia. Definicja dopełnienia jest zależna od kontekstu. Na przykład, dopełnienie zbioru A (oznaczane jako A’) składa się z elementów należących do uniwersum, ale niesklasyfikowanych jako część zbioru A. Suma natomiast łączy wszystkie elementy z obu zbiorów, a różnica identyfikuje te, które są obecne w jednym, ale nie w drugim. Przecięcie dostarcza jedynie wspólnych elementów. Inną istotną różnicą jest kontekst przestrzeni, na której operacje się odbywają. Dopełnienie zbioru zawsze odnosi się do tzw. przestrzeni uniwersalnej. Na przykład, gdy rozważamy liczby całkowite, dopełnienie zbioru liczb parzystych obejmuje każdą liczbę nieparzystą. Z kolei operacje takie jak suma i różnica działają na konkretnych zestawach, co sprawia, że ich wyniki mogą się różnić, zależnie od tych zbiorów. Warto podkreślić, że dopełnienie zbioru pozostaje niezmienne w wyniku innych operacji, zachowując swoje właściwości, takie jak zasady de Morgana. Zrozumienie tych różnic jest kluczowe dla analizy relacji między różnymi zbiorami oraz dla ich zastosowań w różnych dziedzinach matematyki.

Jakie są przykłady dopełnienia zbioru w matematyce?

W matematyce pojęcie dopełnienia zbioru można zobrazować na wiele interesujących sposobów. Na przykład, kiedy mówimy o liczbach, zbiór liczb wymiernych względem liczb rzeczywistych ma za swoje dopełnienie liczby niewymierne. To doskonale ukazuje, jakie bogactwo kryje się w różnych zbiorach oraz ich dopełnieniach.

Innym przykładem jest geometria – w płaszczyźnie euklidesowej, półpłaszczyzna może być uzupełniona poprzez sumę dwóch rozłącznych, otwartych półpłaszczyzn. Rozważmy konkretny zbiór, na przykład U = {1, 2, 3, 4, 5}. Jeśli weźmiemy zbiór A = {1, 3}, to jego dopełnienie A’ to {2, 4, 5}. Ten przypadek dobrze ilustruje zasady rządzące dopełnieniami.

Warto również zauważyć, że dopełnienie zbioru pustego to zbiór uniwersalny, a z kolei dopełnienie zbioru uniwersalnego jest zbiorem pustym. Te przykłady jasno pokazują różnorodność zastosowań dopełnienia oraz znaczenie kontekstu uniwersum w matematyce.

Jakie są praktyczne przykłady dopełnienia zbioru?

Dopełnienie zbioru jest niezwykle przydatne w wielu praktycznych kontekstach, co doskonale ilustruje jego zastosowanie w rzeczywistych sytuacjach. Na przykład:

• podczas filtracji danych w bazie, możemy mieć pełny zestaw klientów oraz odrębny zbór osób, które dokonały zakupu,
• wykorzystanie dopełnienia zbioru kupujących pomoże nam dotrzeć do tych, którzy jeszcze tego nie uczynili, co staje się szczególnie cenne podczas kampanii marketingowych,
• w analizie ryzyka, dopełnienie zdarzenia pozwala na precyzyjne obliczenie prawdopodobieństwa,
• ten aspekt jest kluczowy w dziedzinach takich jak finanse czy ubezpieczenia, gdzie zarządzanie ryzykiem i niepewnością odgrywa fundamentalną rolę,
• w programowaniu, zwłaszcza w języku Python, mamy możliwość zdefiniowania zbioru elementów, które nie spełniają określonych kryteriów.

Dzięki temu z łatwością możemy wykluczyć niepożądane dane z dalszej analizy i przetwarzania. Podobnie w bazach danych SQL, używając zapytań, możemy także uzyskać zbiór rekordów, które nie wpasowują się w ustalone wymagania. Takie działania umożliwiają efektywne zarządzanie danymi i generowanie raportów opartych na konkretnych warunkach. Te różnorodne przykłady doskonale pokazują, jak wszechstronne jest zastosowanie dopełnienia zbioru w różnych dziedzinach, podkreślając jego znaczenie w analizie danych, programowaniu oraz ocenie ryzyka.

Jakie są zastosowania dopełnienia zbioru w matematyce wyższej?

Dopełnienie zbioru znajduje wiele zastosowań w matematyce wyższej i odgrywa kluczową rolę w takich dziedzinach jak:

• teoria mnogości – umożliwia definiowanie skomplikowanych relacji pomiędzy zbiorami, co pozwala lepiej zrozumieć ich wzajemne powiązania,
• topologia – pełni istotną funkcję w badaniu zbiorów otwartych i domkniętych oraz ich charakterystyk,
• analiza matematyczna – stanowi narzędzie do badania funkcji oraz przestrzeni funkcyjnych, a także analizowania zbiorów punktów, które nie wchodzą w zakres danej funkcji,
• teoria miary – kluczowe dla definiowania miary zbiorów oraz przestrzeni mierzalnych,
• prawdopodobieństwo – przy obliczaniu zdarzeń przeciwnych, co jest istotne w takich dziedzinach jak analiza ryzyka, statystyka oraz analiza danych.

Ogólnie rzecz biorąc, dopełnienie zbioru jest fundamentem dla wielu obszarów matematyki i jego zastosowania mają wpływ na różnorodne dziedziny nauki oraz praktycznej działalności.